Research
Silicon quantum electronics
My current research efforts are in modeling the electronic structure and transport properties of silicon nanodevices that incorporate phosphorous atoms with atomic precision. These devices are promising candidates for the solid-state realization of quantum computing technologies, quantum materials, and quantum simulators. We are currently developing theories and codes to describe the many-body physics on these devices. For instance, in arXiv:2402.19392, we developed a protocol for calculating Fermi-Hubbard model parameters from the electronic structure in phosphorus arrays, which is needed to validate quantum simulations on these devices.
Molecular and nanoscale electronics
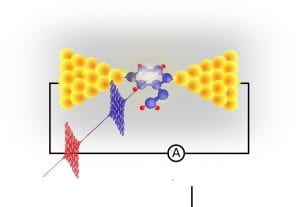My research in this area provides methodologies for the accurate modeling of transport in strongly interacting systems, as well as makes predictions of potential new applications. In Ref. 8, 14, 15. techniques for transport calculations in the language of many-body states (such as Hubbard operators) were developed. These methods provide alternative approaches to other techniques without introducing approximations on the strength of the intramolecular interactions. As an exciting application, In Ref. 10, the pump-probe noise spectroscopy is introduced as a technique that provides information about intramolecular processes and their associated transfer energies.
Quantum thermodynamics
Nanoscale devices operate in a regime where quantum and thermal fluctuations are relevant. Due to their dimension, quantum coherence and other quantum phenomena can affect, in positive or negative forms, their performance. To assess how these conditions determine the efficiency of nanoscale devices, new concepts on thermodynamics are needed. In Refs. 6,7,9,11,12,13, I investigate the same definition of heat and work at this scale and in the strong coupling regime. We also provide theoretical tools to calculate stochastic thermodynamic efficiency, and I find that quantum coherence can significantly modify this.
Graphene-based electromechanical nanosensors
I study analytical models for electromechanical nanoscale sensors under ambient conditions. In particular, I investigate how the environment modifies the mechanical and electrical properties of suspended graphene nanoribbons and their potential application in molecular detection. For more information, see Refs. 3 and 4.
Model theory of metric sheaves
In Ref. 18, I integrate metric model theory and model sheaf theory to describe bundles of finite-dimensional Hilbert spaces and dynamics in smooth manifolds. These results can also be extended to describe quantum mechanical systems in the Schwartz space.
Single-molecule spectroscopy and catalysis
See Refs. 16 and 17.